Modelling human contact networks
Problem: You want to work with a realistic model of a human contact network. What is the appropriate topology?
Solution: This is an active area of research, but a common answer is to use the approach given by Newman [New02], which is to use a powerlaw network with exponential cut-off.
Note
This ensemble of networks is built-in to epydemic in the form
of the PLCNetwork network generator. The details below
explain how this class of networks is constructed.
The theory
A powerlaw network with exponent \(\alpha\) has a degree distibution given by
where \(p_k\) is the probability that a randomly-chosen node in the network will have degree \(k\). This degree distribution has the property that some nodes can have very high degrees with non-zero probability, leading to very large hubs with high centrality. In a population network this would introduce individuals who were massively better connected than the others, which is generally considered undesirable: therre are limits to how many people even the most popular person can actually come into physical contact with.
A powerlaw-with-cutoff network, by contrast, place a limit (denoted \(\kappa\)) on the “likely” highest degree. Up to the cutoff the degree distribution behaves like a powerlaw network; above the cutoff, the probability drops off exponentially quickly, making large hubs highly unlikely. This degree distribution is given by
The following plot shows the difference in the probability of encountering nodes of different degrees under the two distributions.
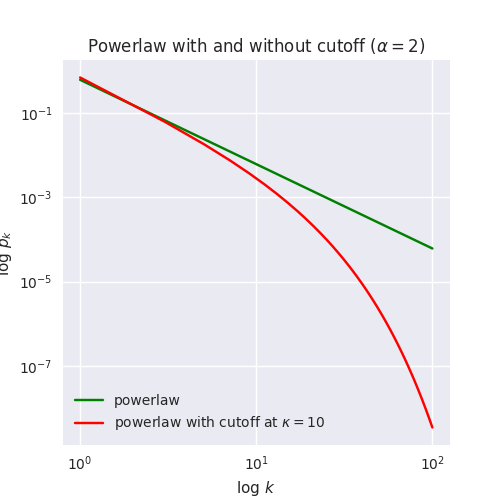
So the probability of finding, for example, a node of degree 100 is \(p_k \approx 0.0001\) under the powerlaw distribution, whereas with a cutoff at \(\kappa = 10\) the probability drops to \(p_k \approx 0.00000001\) – ten thousand times smaller.
Note that these distributions are expressed as proportionalities, because that exposes the essence of what’s going on. To
actually implement the distributions, though, we need to know the constants of proportionality \(\frac{1}{C}\) that normalise the
distribution so that the area under the curve is one. For the powerlaw with
cutoff this constant is built from a polylogarithm, \(C = Li_\alpha(e^{-1 /\kappa})\), a “special” function that’s
fortunately built-into the mpmath package,
so all we need to do is code-up the distribution function in Python. (The equivalent for the powerlaw distribution is
built from the Hurwitz zeta function, \(C = \zeta(\alpha, 1)\).)
The engineering
We can now simply code-up this mathematics, using parameters for the size \(N\) of the network
its exponent \(\alpha\) and cutoff \(\kappa\) to construct a NetworkGenerator for
this class of network:
import networkx
import epydemic
import math
import numpy
from mpmath import polylog
def PowerLawWithCutoffNetwork(epydemic.NetworkGenerator):
N = 'hcn.N' #: Experimental parameter for the order of the network
ALPHA = 'hcn.alpha' #: Experimental parameter for the exponent of the distribution
KAPPA = 'hcn.kappa' #: Experimewntal parameter for the cutoff of the distribution
def __init__(self, params=None, limit=None):
super(PowerLawWithCutoffNetwork, self).__init__(params, limit)
def _makePowerlawWithCutoff(self, alpha, kappa):
'''Create a model function for a powerlaw distribution with exponential cutoff.
:param alpha: the exponent of the distribution
:param kappa: the degree cutoff
:returns: a model function'''
C = polylog(alpha, math.exp(-1.0 / kappa))
def p( k ):
return (pow((k + 0.0), -alpha) * math.exp(-(k + 0.0) / kappa)) / C
return p
def _generateFrom(self, N, p, maxdeg=100):
'''Generate a random graph with degree distribution described
by a model function.
:param N: number of numbers to generate
:param p: model function
:param maxdeg: maximum node degree we'll consider (defaults to 100)
:returns: a network with the given degree distribution'''
rng = numpy.random.default_rng()
ns = []
t = 0
for i in range(N):
while True:
# draw a random degree
k = rng.integers(1, maxdeg)
# do we include a node with this degree?
if rng.random() < p(k):
# yes, add it to the sequence; otherwise,
# draw again
ns.append(k)
t += k
break
# the final sequence of degrees has to sum to an even
# number, as each edge has two endpoints
# if the sequence is odd, remove an element and draw
# another from the distribution, repeating until the
# overall sequence is even
while t % 2 != 0:
# pick a node at random
i = rng.integers(0, len(ns) - 1)
# remove it from the sequence and from the total
t -= ns[i]
del ns[i]
# choose a new node to replace the one we removed
while True:
# draw a new degree from the distribution
k = rng.integers(1, maxdeg)
# do we include a node with this degree?
if rng.random() < p(k):
# yes, add it to the sequence; otherwise,
# draw again
ns.append(k)
t += k
break
# populate the network using the configuration
# model with the given degree distribution
g = networkx.configuration_model(ns,
create_using=networkx.Graph())
return g
def _generate(self, params):
'''Generate the human contact network.
:param params: the experimental parameters
:returns: a network'''
N = params[self.N]
alpha = paramns[self.ALPHA]
kappa = params[self.KAPPA]
return self._generateFrom(N, self._makePowerlawWithCutoff(alpha, kappa))
The _makePowerlawWithCutoff() method just transcribes the
definition of the distribution from above, taking the distribution
parameters \(\alpha\) and \(\kappa\) and returning a model
function that, for any degree \(k\), returns the probability
\(p_k\) of encountering a node of that degree.
The actual construction of the network is done in the
_generateFrom() method using the configuration model, where we
first build a list of \(N\) node degrees by repeatedly drawing
from the powerlaw-with-cutoff distribution. (Actually this function
will construct a network with any desired degree distribution by
defining an appropriate model function.)
The _generate() method unpacks the order, exponent, and cutoff
parameters and passes them to the methods that actually do the work.
You can use this code to create human population models that you then
pass to an experiment (an instance of Dynamics) that runs the
appropriate network process over the network.
The limitations
The reason for the lack of agreement on the structure of human contact networks is due to a detailed feature of the above formulation. If you’re interested, read on….
If you think about your own friends, two of them chosen at random are more likely to be friends of each other than are two people chosen from the population at large: there’s a conditional probability at work that makes people with a mutual friend more likely to be friends of each other. This isn’t always the case – lots of people have largely disjoint sets of friends – but in general the conditional probability is significantly higher than the general population probability.
In a network, this phenomenon manifests itself as clusters in the network: groups of individuals who are more connected than you might expect to each other. Often this manifests itself as triangles of three friends, or even larger clusters for family groups or school classes, where everyone is in contact with everyone else.
The problem that arises is that the configuration model, which we use above to create the network from the degree probabilities, almost never generates these sorts of clusters. The networks it generates are referred to as locally tree-like and don’t have triangles or higher-order clusters. (In fact they don’t have cycles either, which are weaker than clusters.)
This wouldn’t matter except that clustering is now known to affect the spread of epidemic diseases through a population. In a clustered network, if a neighbour of a node becomes infected, then it can infect the node directly (as one would expect) or it can infect one of its other neighbours who then (because of clustering) infects the node – and there might be multiple opportunities for this to happen in a large cluster. The net result is an epidemic that’s larger and faster in the preesence of clustering: not radically different, but definitely observable.
There is a substantial more recent literature on clustered networks that is essential for handling this problem: Miller [Mil09] is a good starting point. Dobson [Dob20] presents a method for creating networks that mimic physical distancing countermeasures to epidemics. Also see Melnik et alia [MHP+11] for a discussion of why clustering often doesn’t matter.